Pariadi's Archives: Deret Mclaurin dan Taylor

Langsung tuju poin aja ya...

Deret Taylor pada bilangan Rill dan bilangan komplex ƒ(x) diuraikan seperti furmula di bawah ini,

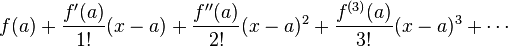
$f(a)+\frac {f'(a)}{1!} (x-a)+ \frac{f''(a)}{2!} (x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+ \cdots$

bilamana kita buat dalam bentuk yg lebih simpel menjadi,

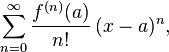
$\sum_{n=0} ^ {\infin } \frac {f^{(n)}(a)}{n!} \, (x-a)^{n},$

dmana n! adalah faktorial n and ƒ⁽ⁿ⁾(a) donasi ke- n derifatif dari ƒ fungsi dari a. The zeroth derivative of ƒ is defined to be ƒ itself and (x − a)⁰ and 0! are both defined to be 1.

Deret Mclaurin :

$f(0)+f'(0)x + \frac{f''(0)}{2!}x^2+\frac{f^{(3)}(0)}{3!}x^3+ \cdots$

gini aja, kalow tmen - temn pengen belajar deret - deret, liat aja di link http://en.wikipedia.org/wiki/Taylor_series cZ lebih lengkap lho....mulai deret - menderet, bilangan exponensial etc....so, met blajar sambil facebook y ( bukan facebook sambil blajar y ngga,,?)

Pariadi's Archives

Deret Mclaurin dan Taylor

Free download