Langsung tuju poin aja ya...
- Deret Taylor pada bilangan Rill dan bilangan komplex ƒ(x) diuraikan seperti furmula di bawah ini,
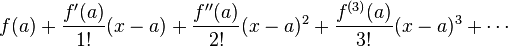
bilamana kita buat dalam bentuk yg lebih simpel menjadi,
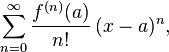
dmana
n! adalah faktorial
n and
ƒ (n)(
a) donasi ke-
n derifatif dari
ƒ fungsi dari
a. The zeroth derivative of
ƒ is defined to be
ƒ itself and
(x − a)0 and 0! are both defined to be 1.
Deret
Mclaurin :

gini aja, kalow tmen - temn pengen belajar deret - deret, liat aja di link
http://en.wikipedia.org/wiki/Taylor_series cZ lebih lengkap lho....mulai deret - menderet, bilangan exponensial etc....so, met blajar sambil facebook y (
bukan facebook sambil blajar y ngga,,?)
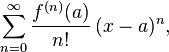




7 komentar:
pertamaxxxx.. wah mantab dh infonya... lanjutkan
sip, thanks dah kunjung
mengingatkan pada FisMat.:D
Apaan ni ya?? gak mudeng aku.. hehehe
Info menarik
Jangan bosan berbagi info lewat blog, karena berbagi itu indah.
VOTE blog ”BIMBINGANMU” pada Djarum Black Blog Competition Vol.2
adi, handak masang iklan yg kada perlu diklikkah??? hanya dipajang ja, pemasukan dapat dari pengunjung yg mengunjungi blog ja. ni linknya, tinggal daftar. http://promoteburner.com/?r=3855
tp mun kawa baisi akun paypal dulu.:D
improved search engine rankings 1 seo backlink service increase backlinks
Posting Komentar